1. 떡볶이 프렌차이즈의 입점전략
- import
import pandas as pd
@
- 작업파일 불러오기
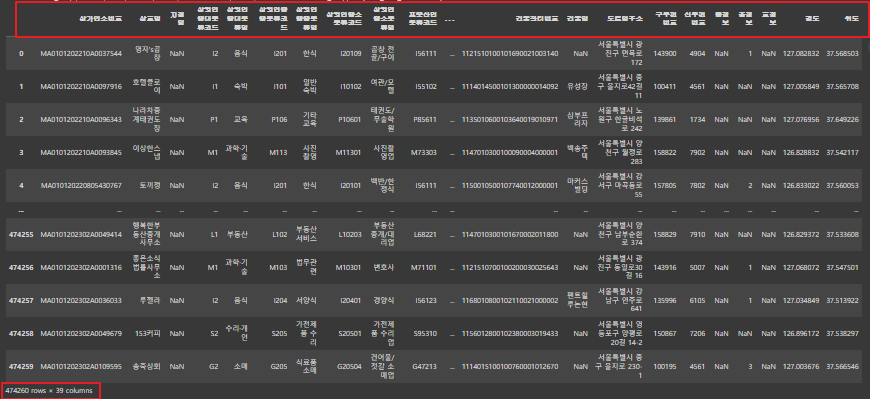
df = pd.read_csv('/content/drive/MyDrive/1. KDT/5. 데이터 분석/데이터/소상공인시장진흥공단_상가(상권)정보_서울_202303.csv')
df
   |
- 데이터 프레임 정보보기
df.info()
 |
- 파리바게트 데이터 필터링
shop = ['엽기떡볶이','죠스떡볶이','신전떡볶이','청년다방','감탄떡볶이']
# 파리바게트 데이터 필터링
# contains() : 특정 문자열 포함 여부에 따라 True, False를 반환
data = df['상호명'].str.contains('파리바게트|파리바게뜨')
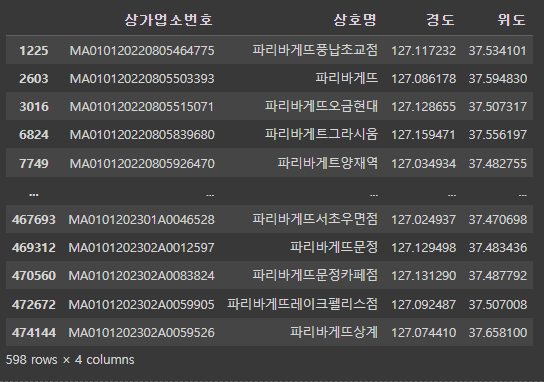
df_paris = df.loc[data, ['상가업소번호','상호명','경도','위도']].copy()
df_paris
 |
- df_paris 데이터프레임의 열 이름을 변경하고, 인덱스를 재설정
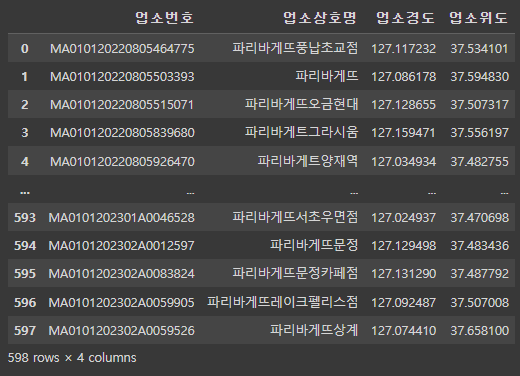
df_paris = df_paris.set_axis(['업소번호','업소상호명','업소경도','업소위도'],axis=1).reset_index(drop=True)
df_paris
 |
- 떡볶이 프랜차이즈 데이터 필터링
# 떡볶이 프랜차이즈 데이터 필터링
df_shop = df.copy()
# 상가업소번호, 상호명, 시군구명, 경도, 위도
# extract() : 특정문자열을 포함하고 있으면 그 문자열을 반환하고, 포함하지 않으면 NaN을 반환
# df_shop['상호명'] = df_shop['상호명'].str.extract('({})'.format('|'.json(shop)))
df_shop['상호명'].str.extract('({})'.format('|'.join(shop)))
 |
- 떡볶이 프랜차이즈 데이터 필터링
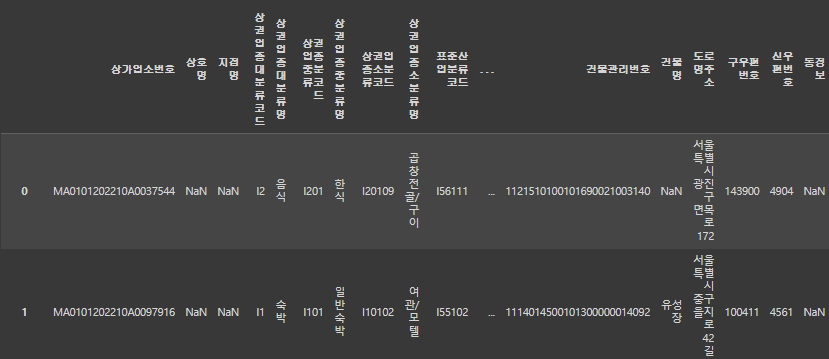
df_shop['상호명'] = df_shop['상호명'].str.extract('({})'.format('|'.join(shop)))[0]
df_shop
 |
- df_shop에서 특정 열(상호명)에 결측치가 있는 행을 제거, 필요한 열만 선택하여 인덱스를 재설정
df_shop = df_shop.dropna(subset=['상호명']).iloc[:, [0, 1, 14, 37, 38]].reset_index(drop=True)
df_shop
 |
- 곱집합 원리
# 곱집합
df1 = pd.DataFrame(['A','B'])
df2 = pd.DataFrame(['가','나','다'])
df1.merge(df2, how='cross')
 |
2. 파버사인 공식
두 지점의 위도와 경도를 입력하며 거릴 구해주는 모듈
- 설치
! pip install haversine
| Collecting haversine Downloading haversine-2.8.1-py2.py3-none-any.whl (7.7 kB) Installing collected packages: haversine Successfully installed haversine-2.8.1 |
- import
from haversine import haversine
- haversine 함수를 사용하여 서울과 파리 간의 거리를 계산,
결과를 킬로미터와 미터 단위로 출력
seoul = [37.541, 126.986]
paris = [48.8567, 2.3508]
print(haversine(seoul,paris, unit='km'))
print(haversine(seoul,paris, unit='m'))
| 8968.562580161477 8968562.580161477 |
- 두 데이터프레임의 곱집합을 생성하기 위해 merge 메서드를 사용, how='cross' 옵션을 사용하여 곱집합을 생성
df_shop.shape
df_paris.shape
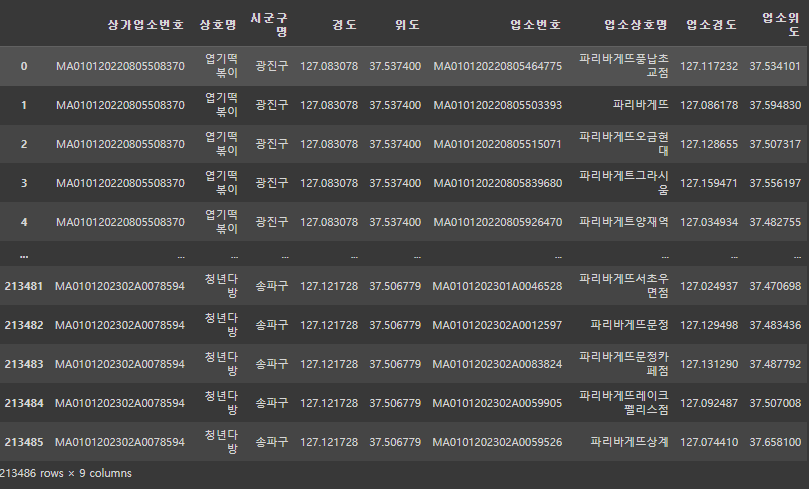
df_cross = df_shop.merge(df_paris, how='cross')
df_cross
  |
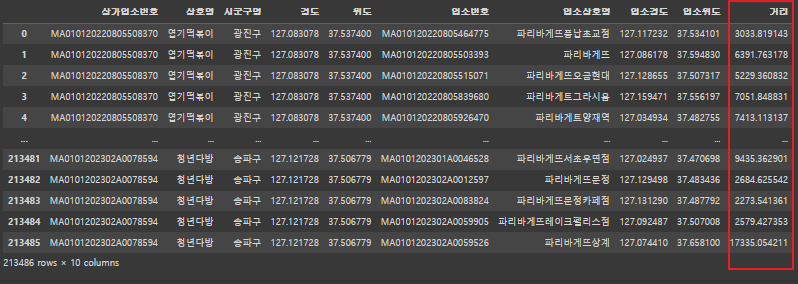
- 기존의 df_cross 데이터프레임에 '거리' 열을 추가
각 행에 대해 위도와 경도를 사용하여 거리를 계산
df_cross['거리'] = df_cross.apply(lambda x: haversine([x['위도'], x['경도']], [x['업소위도'], x['업소경도']], unit='m'), axis=1)
df_cross
 |
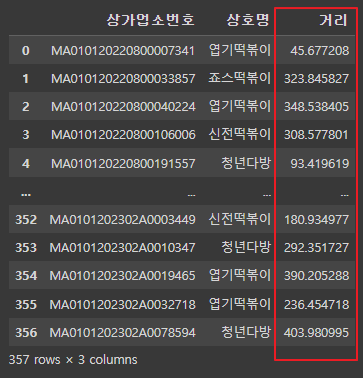
- df_cross 를 '상가업소번호'와 '상호명'으로 그룹화하여 각 그룹에 대해 최소 거리를 계산
'상가업소번호'와 '상호명'으로 그룹화하여 '거리' 열의 최소값을 계산
# 개별 떡볶이 매장과 파리바게트와의 최소거리
df_dis = df_cross.groupby(['상가업소번호','상호명'])['거리'].min().reset_index()
df_dis
 |
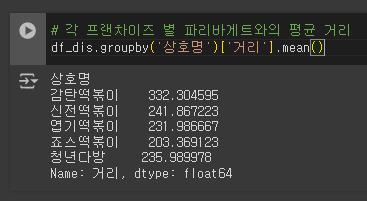
# 각 프랜차이즈 별 파리바게트와의 평균 거리
df_dis.groupby('상호명')['거리'].mean()
 |
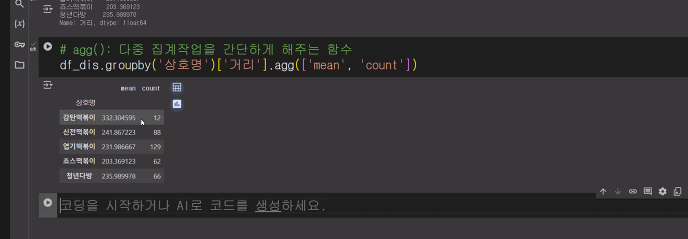
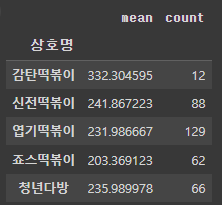
#agg() : 다중 집계 작업을 간단하게 해주는 함수
df_dis.groupby('상호명')['거리'].agg(['mean','count'])
 |
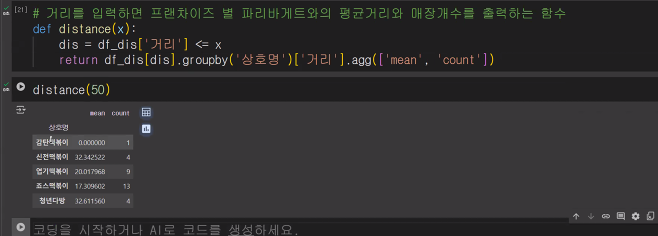
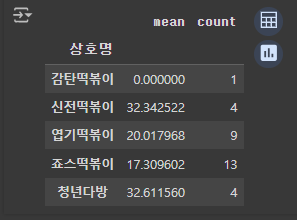
# 거리를 입력하면 프랜차이즈 별 파리바게트와의 평균거리와 매장개수를 출력하는 함수
def distance(x):
dis = df_dis['거리'] <=x
return df_dis[dis].groupby('상호명')['거리'].agg(['mean','count'])
distance(50)
 |
2. 원형그래프 사용하기
- 설치
! pip install pandasecharts
- import
import IPython
from pandasechar ts import echart
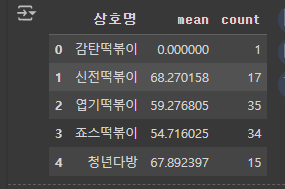
df_100 = distance(100).reset_index()
df_100
 |
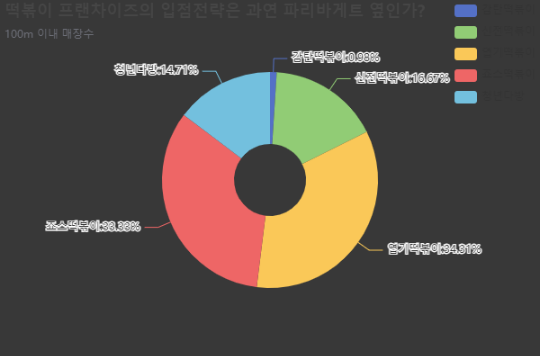
df_100.echart.pie(x='상호명',y='count',figsize=(600,400),
radius=['20%','60%'],label_opts={'position':'outer'},
title='떡볶이 프랜차이즈의 입점전략은 과연 파리바게트 옆인가?',
legend_opts={'pos_right':'0%','orient':'vertical'},
subtitle='100m 이내 매장수').render()
IPython.display.HTML(filename='render.html')
 |
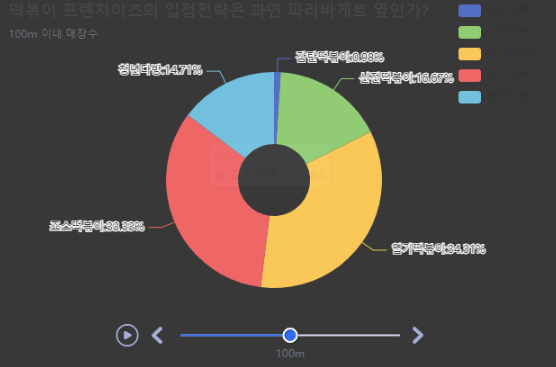
from pyecharts.charts import Timeline, Grid
tl = Timeline({'width':'600px', 'height':'400px'})
pie1 = df_100.echart.pie(x= '상호명', y='count', figsize=(600, 400),
radius=['20%', '60%'], label_opts={'position' : 'outer'},
title = '떡볶이 프렌차이즈의 입점전략은 과연 파리바게트 옆인가?', legend_opts={'pos_right':'0%', 'orient':'vertical'},
subtitle='100m 이내 매장수')
tl.add(pie1, '100m').render()
IPython.display.HTML(filename='render.html')
 |
< js >
tl = Timeline({'width': '600px', 'height': '400px'})
for i in [1000, 100, 50, 30]:
df_d = distance(i).reset_index()
pie1 = df_d.echart.pie(x='상호명', y='count', figsize=(600, 400),
radius=['20%', '60%'], label_opts={'position':'outer'},
title='떡볶이 프렌차이즈의 입점전략은 과연 파리바케트 옆인가?',
legend_opts={'pos_right':'0%', 'orient':'vertical'},
subtitle='{}m 이내 매장수'.format(i))
tl.add(pie1, '{}m'.format(i)).render()
IPython.display.HTML(filename='render.html')
 |
'데이터분석 > 실습' 카테고리의 다른 글
| 05. 데이터분석4 : 서울시 따릉이 API 데이터 활용 (0) | 2024.06.03 |
|---|---|
| 04. 데이터분석3 : 전국 도시공원 데이터 (0) | 2024.05.28 |
| 03. 데이터분석2 : 상권별 업종 밀집 통계 데이터 (0) | 2024.05.28 |
| 02. 데이터분석1 : 가상 온라인 쇼핑몰 데이터 활용 (0) | 2024.05.27 |
| 01. Matplotlib (0) | 2024.05.27 |