05. 딥러닝

1. 뉴런(neuron)

 

 

1. 생물학적 뉴런

* 인간의 뇌는 수십억 개의 뉴런을 가지고 있음 * 뉴런은 화학적, 전기적 신호를 처리하고 전달하는 연결된 뇌신경 세포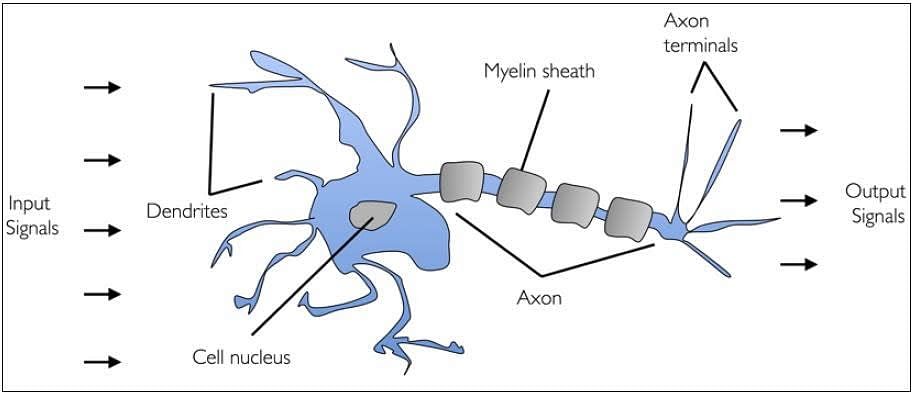

2. 인공 뉴런(Perceptron)

* 1943년에 워렌 맥컬록, 월터 피츠 단순화된 뇌세포 개념을 발표 * 신경 세포를 이진 출력을 가진 단순한 논리 게이트라고 설명 * 생물학적 뉴런의 모델에 기초한 수학적 기능으로, 각 뉴런이 입력을 받아 개별적으로 가중치를 곱하여 나온 합계를 비선형 함수를 전달하여 출력을 생성

 

2. 퍼셉트론(Perceptron)

* 인공 신경망의 가장 기본적인 형태로 1957년에 처음 소개됨
* 입력과 출력을 가진 단일 뉴런 모델을 기반
* 초기에 기계 학습 알고리즘 중 하나로 이진 분류 문제를 해결하기 위해 설계

 

• import

import torch         import torch.nn as nn         import torch.optim as optim

 

 

1. 논리 회귀(단층 퍼셉트론)로 AND / OR 문제 풀기

 

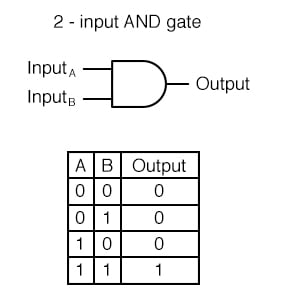• AND 게이트를 학습하는 단순 논리 회귀 모델을 구현하고 학습

# AND 게이트 (하나라도 False면 False)               X = torch.FloatTensor([[0, 0], [0, 1], [1, 0], [1, 1]])           y = torch.FloatTensor([[0], [0], [0], [1]])           model = nn.Sequential(               nn.Linear(2, 1),               nn.Sigmoid()  # Sotmax가 아니기 때문에 직접 확률을 구하는 Sigmoid()를 넣어주어야 함           )           # 학습           optimizer = optim.SGD(model.parameters(), lr=1)           epochs = 1000           for epoch in range(epochs + 1):             y_pred = model(X)             loss = nn.BCELoss()(y_pred, y)  # 단순 논리 회귀의 loss             optimizer.zero_grad()             loss.backward()             optimizer.step()             if epoch % 100 == 0:               y_bool = (y_pred >= 0.5).float()               accuracy = (y == y_bool).float().sum() / len(y) * 100               print(f'Epoch: {epoch:4d}/{epochs} Loss: {loss:.6f} Accuracy: {accuracy:.2f}%')

Epoch:    0/1000 Loss: 0.824187 Accuracy: 25.00% Epoch:  100/1000 Loss: 0.143643 Accuracy: 100.00% Epoch:  200/1000 Loss: 0.081609 Accuracy: 100.00% Epoch:  300/1000 Loss: 0.056502 Accuracy: 100.00% Epoch:  400/1000 Loss: 0.043025 Accuracy: 100.00% Epoch:  500/1000 Loss: 0.034662 Accuracy: 100.00% Epoch:  600/1000 Loss: 0.028983 Accuracy: 100.00% Epoch:  700/1000 Loss: 0.024883 Accuracy: 100.00% Epoch:  800/1000 Loss: 0.021788 Accuracy: 100.00% Epoch:  900/1000 Loss: 0.019370 Accuracy: 100.00% Epoch: 1000/1000 Loss: 0.017431 Accuracy: 100.00%

• 주석

1. 데이터 준비:
   • 입력 데이터 X는 AND 게이트를 나타내는 2차원 벡터입니다.
   • 출력 데이터 y는 AND 연산에 대한 결과를 나타내는 1차원 벡터입니다.

 

1. 모델 정의:
   • nn.Sequential을 사용하여 입력 차원이 2이고 출력 차원이 1인 선형 레이어를 포함하는 모델을 정의합니다.
   • 마지막 레이어로 nn.Sigmoid()를 추가하여 이진 분류 문제에서 확률을 계산할 수 있습니다.

 

1. 손실 함수 및 최적화:
   • 손실 함수로 이진 교차 엔트로피 손실(nn.BCELoss())을 사용합니다. 이 함수는 이진 분류 문제에서 확률 예측과 실제 값 간의 손실을 계산합니다.
   • 최적화 알고리즘으로 확률적 경사 하강법(SGD)을 사용하며, 학습률은 1로 설정합니다.

 

1. 학습 과정:
   • 주어진 epoch 수(여기서는 1000)만큼 반복하여 모델을 학습합니다.
   • 각 epoch 마다:
     • model(X)를 사용하여 예측값 y_pred를 계산합니다.
     • nn.BCELoss()(y_pred, y)를 사용하여 예측값과 실제 값 사이의 손실을 계산합니다.
     • optimizer.zero_grad()로 기울기를 초기화하고, loss.backward()로 역전파를 수행합니다.
     • optimizer.step()으로 파라미터를 업데이트합니다.
     • 매 100번째 epoch 마다 손실(Loss)과 정확도(Accuracy)를 출력합니다.

 

• OR 게이트를 학습하는 단순 논리 회귀 모델을 구현하고 학습

# OR 게이트 (하나라도 True면 True)         X = torch.FloatTensor([[0, 0], [0, 1], [1, 0], [1, 1]])         y = torch.FloatTensor([[0], [1], [1], [1]])         model = nn.Sequential(             nn.Linear(2, 1),             nn.Sigmoid()  # Sotmax가 아니기 때문에 직접 확률을 구하는 Sigmoid()를 넣어주어야 함         )         optimizer = optim.SGD(model.parameters(), lr=1)         epochs = 1000         for epoch in range(epochs + 1):           y_pred = model(X)           loss = nn.BCELoss()(y_pred, y)  # 단순 논리 회귀의 loss           optimizer.zero_grad()           loss.backward()           optimizer.step()           if epoch % 100 == 0:             y_bool = (y_pred >= 0.5).float()             accuracy = (y == y_bool).float().sum() / len(y) * 100             print(f'Epoch: {epoch:4d}/{epochs} Loss: {loss:.6f} Accuracy: {accuracy:.2f}%')

Epoch:    0/1000 Loss: 0.632454 Accuracy: 50.00% Epoch:  100/1000 Loss: 0.091876 Accuracy: 100.00% Epoch:  200/1000 Loss: 0.047625 Accuracy: 100.00% Epoch:  300/1000 Loss: 0.031766 Accuracy: 100.00% Epoch:  400/1000 Loss: 0.023733 Accuracy: 100.00% Epoch:  500/1000 Loss: 0.018907 Accuracy: 100.00% Epoch:  600/1000 Loss: 0.015696 Accuracy: 100.00% Epoch:  700/1000 Loss: 0.013409 Accuracy: 100.00% Epoch:  800/1000 Loss: 0.011700 Accuracy: 100.00% Epoch:  900/1000 Loss: 0.010374 Accuracy: 100.00% Epoch: 1000/1000 Loss: 0.009317 Accuracy: 100.00%

• 주석

1. 데이터 준비:
   • 입력 데이터 X는 AND 게이트를 나타내는 2차원 벡터입니다.
   • 출력 데이터 y는 AND 연산에 대한 결과를 나타내는 1차원 벡터입니다.

 

1. 모델 정의:
   • nn.Sequential을 사용하여 입력 차원이 2이고 출력 차원이 1인 선형 레이어를 포함하는 모델을 정의합니다.
   • 마지막 레이어로 nn.Sigmoid()를 추가하여 이진 분류 문제에서 확률을 계산할 수 있습니다.

 

1. 손실 함수 및 최적화:
   • 손실 함수로 이진 교차 엔트로피 손실(nn.BCELoss())을 사용합니다. 이 함수는 이진 분류 문제에서 확률 예측과 실제 값 간의 손실을 계산합니다.
   • 최적화 알고리즘으로 확률적 경사 하강법(SGD)을 사용하며, 학습률은 1로 설정합니다.

 

1. 학습 과정:
   • 주어진 epoch 수(여기서는 1000)만큼 반복하여 모델을 학습합니다.
   • 각 epoch 마다:
     • model(X)를 사용하여 예측값 y_pred를 계산합니다.
     • nn.BCELoss()(y_pred, y)를 사용하여 예측값과 실제 값 사이의 손실을 계산합니다.
     • optimizer.zero_grad()로 기울기를 초기화하고, loss.backward()로 역전파를 수행합니다.
     • optimizer.step()으로 파라미터를 업데이트합니다.
     • 매 100번째 epoch 마다 손실(Loss)과 정확도(Accuracy)를 출력합니

 

 

2. 논리회귀(단층 퍼셉트론)로 XOR문제 풀기

 

• XOR 문제를 해결하기 위한 단순 논리 회귀 모델을 구현하고 학습

X = torch.FloatTensor([[0, 0], [0, 1], [1, 0], [1, 1]])           y = torch.FloatTensor([[0], [1], [1], [0]])           model = nn.Sequential(               nn.Linear(2, 1),               nn.Sigmoid()  # Sotmax가 아니기 때문에 직접 확률을 구하는 Sigmoid()를 넣어주어야 함           )           optimizer = optim.SGD(model.parameters(), lr=1)           epochs = 1000           for epoch in range(epochs + 1):             y_pred = model(X)             loss = nn.BCELoss()(y_pred, y)  # 단순 논리 회귀의 loss             optimizer.zero_grad()             loss.backward()             optimizer.step()             if epoch % 100 == 0:               y_bool = (y_pred >= 0.5).float()               accuracy = (y == y_bool).float().sum() / len(y) * 100               print(f'Epoch: {epoch:4d}/{epochs} Loss: {loss:.6f} Accuracy: {accuracy:.2f}%')

Epoch:    0/1000 Loss: 0.700468 Accuracy: 50.00% Epoch:  100/1000 Loss: 0.693149 Accuracy: 25.00% Epoch:  200/1000 Loss: 0.693147 Accuracy: 25.00% Epoch:  300/1000 Loss: 0.693147 Accuracy: 25.00% Epoch:  400/1000 Loss: 0.693147 Accuracy: 50.00% Epoch:  500/1000 Loss: 0.693147 Accuracy: 50.00% Epoch:  600/1000 Loss: 0.693147 Accuracy: 50.00% Epoch:  700/1000 Loss: 0.693147 Accuracy: 50.00% Epoch:  800/1000 Loss: 0.693147 Accuracy: 50.00% Epoch:  900/1000 Loss: 0.693147 Accuracy: 50.00% Epoch: 1000/1000 Loss: 0.693147 Accuracy: 50.00%

• 주석

1. 데이터 준비:
   • 입력 데이터 X는 XOR 문제를 나타내는 2차원 벡터입니다.
   • 출력 데이터 y는 XOR 연산에 대한 결과를 나타내는 1차원 벡터입니다.

 

1. 모델 정의:
   • nn.Sequential을 사용하여 입력 차원이 2이고 출력 차원이 1인 선형 레이어를 포함하는 모델을 정의합니다.
   • 마지막 레이어로 nn.Sigmoid()를 추가하여 이진 분류 문제에서 확률을 계산할 수 있습니다.
   •  

1. 손실 함수 및 최적화:
   • 손실 함수로 이진 교차 엔트로피 손실(nn.BCELoss())을 사용합니다. 이 함수는 이진 분류 문제에서 확률 예측과 실제 값 간의 손실을 계산합니다.
   • 최적화 알고리즘으로 확률적 경사 하강법(SGD)을 사용하며, 학습률은 1로 설정합니다.

 

1. 학습 과정:
   • 주어진 epoch 수(여기서는 1000)만큼 반복하여 모델을 학습합니다.
   • 각 epoch 마다:
     • model(X)를 사용하여 예측값 y_pred를 계산합니다.
     • nn.BCELoss()(y_pred, y)를 사용하여 예측값과 실제 값 사이의 손실을 계산합니다.
     • optimizer.zero_grad()로 기울기를 초기화하고, loss.backward()로 역전파를 수행합니다.
     • optimizer.step()으로 파라미터를 업데이트합니다.
     • 매 100번째 epoch 마다 손실(Loss)과 정확도(Accuracy)를 출력합니다.

 

1. 결과 해석:
   • 학습 과정에서 출력되는 Loss는 각 epoch에서의 손실 값이며, Accuracy는 현재 모델의 정확도를 나타냅니다.
   • XOR 문제를 해결하는 데 필요한 손실 감소와 정확도 향상을 확인할 수 있습니다.

이 코드는 단순 논리 회귀를 사용하여 XOR 문제를 해결하는 방법을 보여줍니다. nn.Sigmoid()를 통해 확률을 계산하고, 이진 교차 엔트로피 손실을 최소화하여 모델을 학습합니다.

 

 

3. 다층 퍼셉트론으로 XOR문제 풀기

* 여러개의 은닉층을 만들어 해결 * https://colah.github.io/posts/2015-09-NN-Types-FP/

 

• PyTorch를 사용하여
  여러 개의 선형 레이어와 Sigmoid 활성화 함수를 사용하여 구성된 신경망 모델을 정의

model = nn.Sequential(             nn.Linear(2, 64),   # 입력 차원 2, 출력 차원 64인 선형 레이어             nn.Sigmoid(),       # 첫 번째 Sigmoid 활성화 함수 (출력층 X, 은닉층 O)             nn.Linear(64, 32),  # 입력 차원 64, 출력 차원 32인 선형 레이어             nn.Sigmoid(),       # 두 번째 Sigmoid 활성화 함수 (출력층 X, 은닉층 O)             nn.Linear(32, 16),  # 입력 차원 32, 출력 차원 16인 선형 레이어             nn.Sigmoid(),       # 세 번째 Sigmoid 활성화 함수 (출력층 X, 은닉층 O)             nn.Linear(16, 1),   # 입력 차원 16, 출력 차원 1인 선형 레이어             nn.Sigmoid()        # 네 번째 Sigmoid 활성화 함수 (출력층, 최종 출력을 위한 Sigmoid)         )         print(model)

모델 구조 nn.Sequential: 순차적으로 레이어를 쌓는 모델을 정의 nn.Linear(in_features, out_features): 선형 변환을 수행하는 레이어                                                           입력 차원(in_features)과 출력 차원(out_features)을 지정 nn.Sigmoid(): Sigmoid 활성화 함수를 레이어에 추가하여 출력을 0과 1 사이의 확률값으로 변환합니다. 모델 구성 첫 번째 레이어 입력 차원: 2 | 출력 차원: 64 | 활성화 함수: Sigmoid 역할: 입력 데이터를 받아 64차원의 출력을 생성 두 번째 레이어 입력 차원: 64 | 출력 차원: 32 | 활성화 함수: Sigmoid 역할: 이전 레이어의 출력을 입력으로 받아 32차원의 출력을 생성 세 번째 레이어 입력 차원: 32 | 출력 차원: 16 | 활성화 함수: Sigmoid 역할: 이전 레이어의 출력을 입력으로 받아 16차원의 출력을 생성 네 번째 레이어 입력 차원: 16 | 출력 차원: 1 | 활성화 함수: Sigmoid 역할: 최종 출력을 위해 1차원의 출력을 생성, 이 레이어의 출력은 최종 예측값을 나타냅니다. 요약 이 모델은 총 4개의 선형 레이어와 그 사이에 Sigmoid 활성화 함수를 사용하여 구성되어 있습니다. 입력 차원은 2이고, 최종 출력은 1차원으로 설정되어 있습니다. 이 구조는 입력 데이터로부터 복잡한 비선형 관계를 학습할 수 있는 다층 신경망의 기본 구조를 갖추고 있습니다.

[ nn.Sequential 모델을 출력 ] Sequential(   (0): Linear(in_features=2, out_features=64, bias=True)   (1): Sigmoid()   (2): Linear(in_features=64, out_features=32, bias=True)   (3): Sigmoid()   (4): Linear(in_features=32, out_features=16, bias=True)   (5): Sigmoid()   (6): Linear(in_features=16, out_features=1, bias=True)   (7): Sigmoid() ) ------------------------------------------------------- 첫 번째 레이어 (Linear 레이어) 입력 차원: 2 | 출력 차원: 64 편향(bias) 포함 여부: True 두 번째 레이어 (Sigmoid 활성화 함수) 입력: 이전 Linear 레이어의 출력 출력: Sigmoid 함수를 통과한 값 세 번째 레이어 (Linear 레이어) 입력 차원: 64 | 출력 차원: 32 편향(bias) 포함 여부: True 네 번째 레이어 (Sigmoid 활성화 함수) 입력: 이전 Linear 레이어의 출력 출력: Sigmoid 함수를 통과한 값 다섯 번째 레이어 (Linear 레이어) 입력 차원: 32 | 출력 차원: 16 편향(bias) 포함 여부: True 여섯 번째 레이어 (Sigmoid 활성화 함수) 입력: 이전 Linear 레이어의 출력 출력: Sigmoid 함수를 통과한 값 일곱 번째 레이어 (Linear 레이어) 입력 차원: 16 | 출력 차원: 1 편향(bias) 포함 여부: True 여덟 번째 레이어 (Sigmoid 활성화 함수) 입력: 이전 Linear 레이어의 출력 출력: Sigmoid 함수를 통과한 값, 최종 출력 이 모델은 주어진 입력 데이터에 대해 각 레이어를 순차적으로 통과시키며, 각 레이어의 출력을 Sigmoid 활성화 함수를 통과시켜 비선형성을 추가한 후 최종적으로 출력을 계산하는 구조를 가지고 있습니다.

 

 

• XOR 게이트를 학습하는 단순 논리 회귀 모델을 구현하고 학습

X = torch.FloatTensor([[0, 0], [0, 1], [1, 0], [1, 1]])           y = torch.FloatTensor([[0], [1], [1], [0]])           # 학습           optimizer = optim.SGD(model.parameters(), lr=1)           epochs = 1000           for epoch in range(epochs + 1):             y_pred = model(X)             loss = nn.BCELoss()(y_pred, y)  # 단순 논리 회귀의 loss             optimizer.zero_grad()             loss.backward()             optimizer.step()             if epoch % 100 == 0:               y_bool = (y_pred >= 0.5).float()               accuracy = (y == y_bool).float().sum() / len(y) * 100               print(f'Epoch: {epoch:4d}/{epochs} Loss: {loss:.6f} Accuracy: {accuracy:.2f}%')

Epoch:    0/1000 Loss: 0.702334 Accuracy: 50.00% Epoch:  100/1000 Loss: 0.693155 Accuracy: 50.00% Epoch:  200/1000 Loss: 0.693145 Accuracy: 50.00% Epoch:  300/1000 Loss: 0.693135 Accuracy: 50.00% Epoch:  400/1000 Loss: 0.693125 Accuracy: 50.00% Epoch:  500/1000 Loss: 0.693115 Accuracy: 50.00% Epoch:  600/1000 Loss: 0.693104 Accuracy: 75.00% Epoch:  700/1000 Loss: 0.693092 Accuracy: 50.00% Epoch:  800/1000 Loss: 0.693078 Accuracy: 50.00% Epoch:  900/1000 Loss: 0.693063 Accuracy: 50.00% Epoch: 1000/1000 Loss: 0.693046 Accuracy: 75.00%

 

• 주석

1. 데이터 준비:
   • 입력 데이터 X는 XOR 게이트를 나타내는 2차원 벡터입니다.
   • 출력 데이터 y는 XOR 연산에 대한 결과를 나타내는 1차원 벡터입니다.

 

1. 모델 정의:
   • nn.Sequential을 사용하여 입력 차원이 2이고 출력 차원이 1인 선형 레이어를 포함하는 모델을 정의합니다.
   • 마지막 레이어로 nn.Sigmoid()를 추가하여 이진 분류 문제에서 확률을 계산할 수 있습니다.

 

1. 손실 함수 및 최적화:
   • 손실 함수로 이진 교차 엔트로피 손실(nn.BCELoss())을 사용합니다. 이 함수는 이진 분류 문제에서 확률 예측과 실제 값 간의 손실을 계산합니다.
   • 최적화 알고리즘으로 확률적 경사 하강법(SGD)을 사용하며, 학습률은 1로 설정합니다.

 

1. 학습 과정:
   • 주어진 epoch 수(여기서는 1000)만큼 반복하여 모델을 학습합니다.
   • 각 epoch 마다:
     • model(X)를 사용하여 예측값 y_pred를 계산합니다.
     • nn.BCELoss()(y_pred, y)를 사용하여 예측값과 실제 값 사이의 손실을 계산합니다.
     • optimizer.zero_grad()로 기울기를 초기화하고, loss.backward()로 역전파를 수행합니다.
     • optimizer.step()으로 파라미터를 업데이트합니다.
     • 매 100번째 epoch 마다 손실(Loss)과 정확도(Accuracy)를 출력합니다.

 

1. 결과 해석:
   • XOR 게이트는 단순 논리 회귀 모델로는 선형적으로 분리할 수 없기 때문에, 이 코드는 XOR 문제를 해결하지 못할 것입니다. 실제로 코드를 실행하면 학습 과정에서 정확도가 낮거나 손실이 줄어들지 않는 것을 확인할 수 있습니다.
   • XOR 문제를 해결하려면 단순 논리 회귀보다는 신경망을 깊게 쌓거나 비선형 활성화 함수(예: nn.ReLU(), nn.Tanh() 등)를 사용하는 방법이 필요합니다.

따라서, 위 코드는 XOR 게이트 문제를 단순 논리 회귀로 접근하여 해결하는 것이 아니라, XOR 문제의 복잡성을 이해하기 위한 예시로 보실 수 있습니다.